회귀 모델이 풀 수 없는 문제
이번 아티클에서는 회귀모델(Regression Model)이 어떤 경우에 저조한 성과를 내는지, 더 나아가 Dataset이 어떤 특성을 지닐 때 회귀모델로 해당 문제를 풀어낼 수 없는지 필자가 경험한 바를 서술해보고자 한다.
CONTENTS
- Introduction
- 프로젝트 배경과 주제
- 2.1. 연구 주제
- 2.2. 산업 현황 및 연구 목적
- 2.3. 연구 문제 및 실험 정의
- 데이터 소개와 변수 정의
- 3.1. 데이터 톺아보기
- 3.2. 122,400개의 인스턴스로 구성된 데이터
- 3.3. 변수 정의
- Data Preprocessing & EDA
- 4.1. 변수명 Renaming
- 4.2. Data Preprocessing
- 4.3. EDA
- Modeling
- 5.1. Simple Linear Regression (v1)
- 5.2. Simple Linear Regression (v2) — “day” 변수 제외
- 5.3. Polynomial Regression (v1) — “degree=2”
- 5.4. Polynomial Regression (v2) — “degree=3”
- 5.5. Polynomial Regression (v3) — “degree=4”
- 5.6. Polynomial Regression (v4) — “degree=5”
- Conclusion
- 6.1. Regression Model 외의 모델이 필요하다!
- 6.2. Regression Model이 해당 Dataset 학습에 적절한 모델이 아님을 파악하는 방법은?

1. Introduction
머신러닝과 딥러닝 알고리즘을 공부하신 분들이라면 누구나 아는 이야기이지만, 데이터 사이언스에서 가장 중요한 지침이 있다.
“어느 특정 모델이 모든 경우에 항상 우월한 퍼포먼스를 지니지 않는다.”
즉, 아무리 복잡하고 인기가 많은 모델이더라도 데이터셋의 특성에 따라 우월한 Metric을 낳을 수도 있고, 혹은 저조한 Metric을 낳을 수도 있다. (그래서 모델링 작업에서 가장 중요한 것은 다름 아닌, Dataset에 대한 이해이기도 하다.)
이번 아티클에서는 회귀모델(Regression Model)이 어떤 경우에 저조한 성과를 내는지, 더 나아가 Dataset이 어떤 특성을 지닐 때 회귀모델로 해당 문제를 풀어낼 수 없는지 필자가 경험한 바를 서술해보고자 한다.
회귀모델 학습 실험을 하다가 우연히 직관적으로 알게 된 추측성 결론이었지만, 통계학 교수님으로부터 타당성을 인정 받았기 때문에 본 내용은 충분히 공개해도 되리라 생각한다. (교수님, 사랑합니다.)
2. 프로젝트 배경과 주제
2.1. 연구 주제
“기상 정보를 통한 전력 사용량 예측 모델 구축하기”
2.2. 산업 현황 및 연구 목적
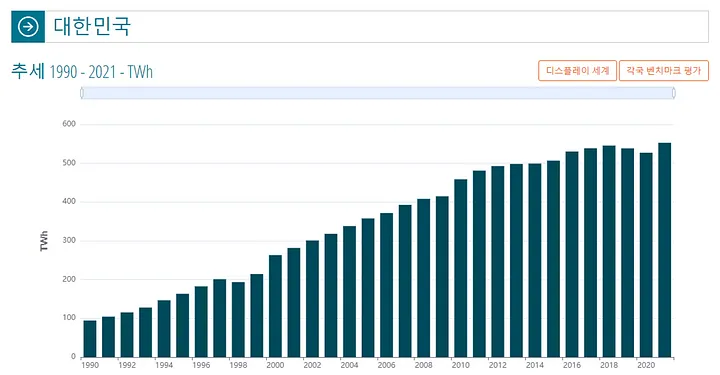
(1) 한국의 전력 사용량은 매해 증가하는 추세
- 30년 전 대비 5배 이상 높아진 수준
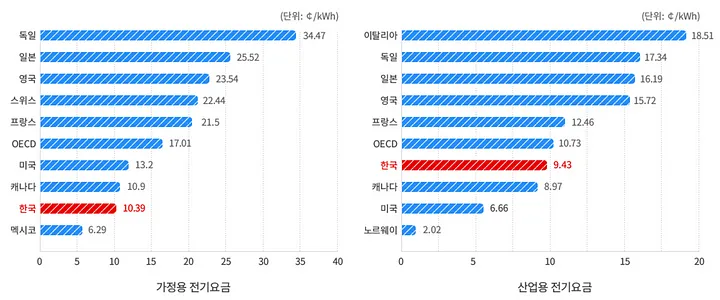
(2) 한국의 전기료는 OECD 회원국들의 50%에 미치지 못할 정도로 저렴한 수준
- 전력 사용량은 증가하는 반면, 상대적으로 낮게 책정된 전기료 수준
- 에너지 비용 모니터링 & 예측 서비스를 도입하여 시장경쟁력 확보의 필요성
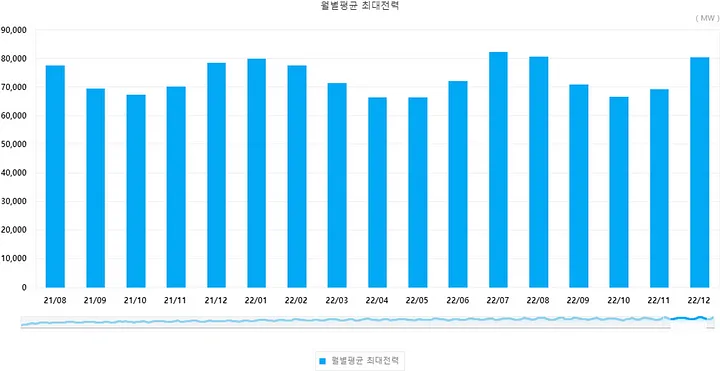
(3) 한국의 전력 사용량은 여름철 증가하는 계절적 주기성이 존재함
- 공급량 조절이 쉽지 않은 도메인 특성을 고려했을 때, 전력 사용량을 예측하여 효율적인 에너지 관리 방안 도입의 필요성
2.3. 연구 문제 및 실험 정의
“기상 데이터를 통해 전력사용량 예측 모델을 설계하고자 한다.”
전력사용량 ~ 기온
전력사용량 ~ 풍속
전력사용량 ~ 습도
전력사용량 ~ 강수량
전력사용량 ~ 일조
전력사용량 ~ (건물 내) 비전기냉방설비운영 여부
전력사용량 ~ (건물 내) 태양광 보유 여부
3. 데이터 소개와 변수 정의
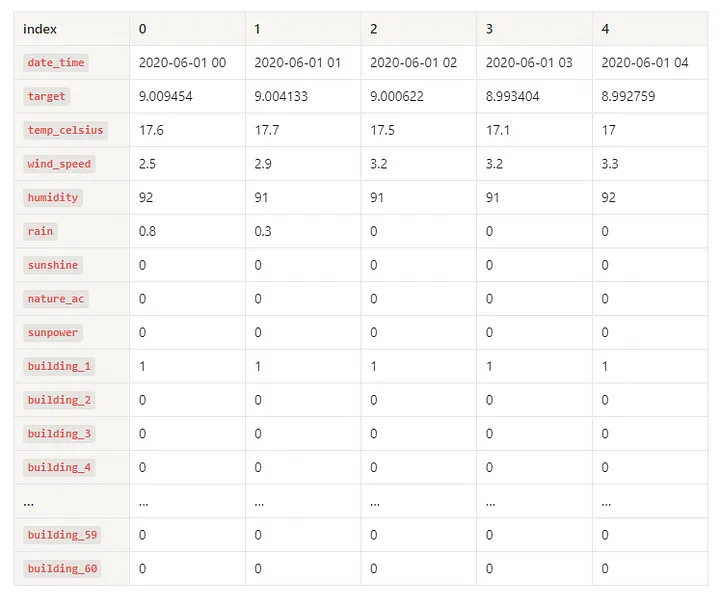
3.1. 데이터 톺아보기
df.head()
.webp)
df.tail()
.webp)
3.2. 122,400개의 인스턴스로 구성된 데이터
- 60개의 건물별 (
num)로 구성 - 2020년 6월 1일부터 2020년 8월 24일까지의 엔지니어링 데이터로 구성
- 측정 데이터의 Unit: 1시간
3.3. 변수 정의
| 변수 | 설명 | 변수 타입 |
|---|---|---|
num |
건물번호 (1<= Integer <= 60) | x |
date_time |
YYYY-MM-DD HH | x |
전력사용량(kWh) |
전력사용량 (킬로와트시) | y |
기온(°C) |
섭씨 기온 (Celsius Degree) | x |
풍속(m/s) |
풍속 (초당 미터 속도) | x |
습도(%) |
습도 | x |
강수량(mm) |
강수량 | x |
일조(hr) |
1시간 중 일조량이 존재한 시간 (0.0 <= Float <= 1.0) | x |
비전기냉방설비운영 |
운영 여부 Boolean 표현 (0: False, 1: True) | x |
태양광보유 |
보유 여부 Boolean 표현 (0: False, 1: True) | x |
4. Data Preprocessing & EDA
4.1. 변수명 Renaming
| AS-IS | TO-BE |
|---|---|
num |
building_num |
date_time |
date_time |
전력사용량(kWh) |
target |
기온(°C) |
temp_celsius |
풍속(m/s) |
wind_speed |
습도(%) |
humidity |
강수량(mm) |
rain |
일조(hr) |
sunshine |
비전기냉방설비운영 |
nature_ac |
태양광보유 |
sunpower |
고통스러운 한글 인코딩 문제는 언제 어디에서 터질지 모른다.
4.2. Data Preprocessing
(1) target (전력사용량)
target의 분포: “Positive Skewness” (양의 왜도, 오른쪽 꼬리가 길다.)- Model Fitting의 효과를 향상시키기 위해, 다음과 같이 변환하자.
# Train할 때
target = np.log(1 + target)
# Predict할 때
target = np.exp(target) - 1
[변환 전] Distribution of Target Values
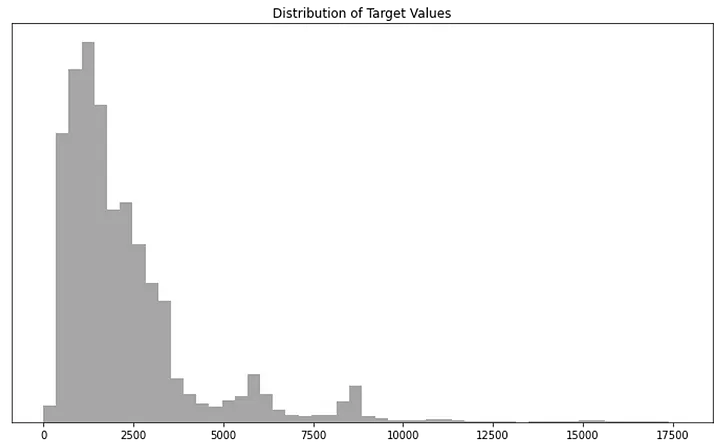
이러한 분포는 자연현상과 사회현상에서 흔히 나타나는데, Model의 Overfitting 문제에 매우 취약하다.
[변환 후] Distribution of Target Values
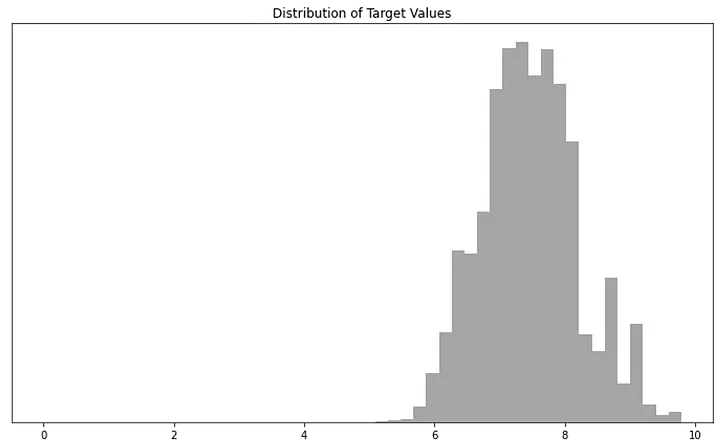
Gotcha! 어느 정도 정규성을 확보했군…
(2) building_num (건물번호)
- Integer Type (1 ≤
building_num≤ 60) - 도메인 지식을 고려했을 때, 건물 별로 전력 설계 파이프라인, 건물의 위치 등에 따라 전력사용량이 국지적으로 큰 차이가 발생할 것이다.
각 60개 building_num별 Distribution of Target Values
if skewness >= 1.5:
color = 'red'
elif skewness < -1.5:
color = 'blue'
else:
color = 'grey'

1부터 60까지는 Ordinal이라기보다는, Cardinal한 Label이므로, 모델이 값의 우열이 있는 것으로 오해할 수 있다. 그래서 One Hot Encoding을 통해 각 building_num을 dummy화하도록 한다.
building_num이 사라지고,building_#의 Scarse Vectors로 대체되었다.
(3) date_time (YYYY-MM-DD HH)
- YYYY-MM-DD HH 포맷이 String data type으로 되어 있으므로, 이를 변환해야 한다.
Year,Month,Day,Hour: 기상 혹은 기후 현상과 상관성이 있는 정보- Day of Week (DoW):
date_time에는 직접적으로 표기되어 있지 않으나, 전력사용량의 주기성을 지니고 있는 정보이므로 새롭게 생성하도록 한다. - 본 Dataset에서는
Year가 ‘2020’ 한 가지만 존재하므로,Year변수는 삭제하도록 한다.
변환 결과
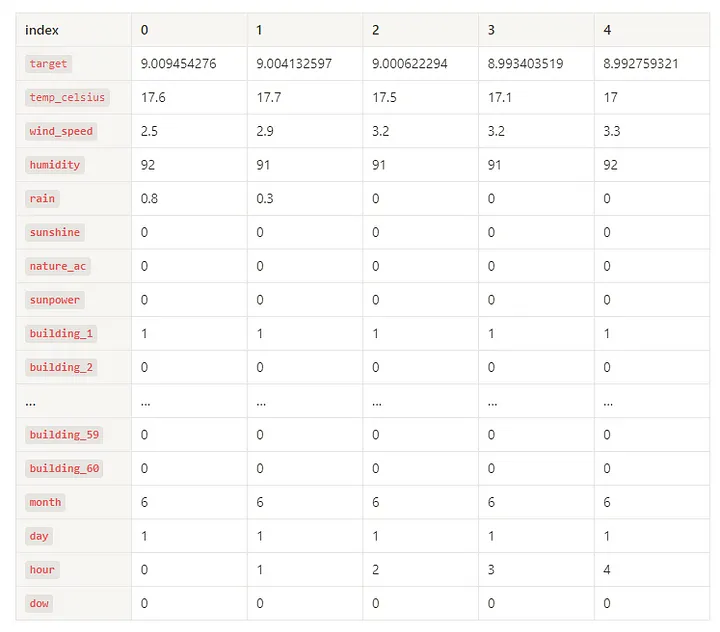
date_time은 사라지고,month,day,hour,dow가 생성되었다.
4.3. EDA
(1) Correlation Coefficient (상관계수)
Heat Map
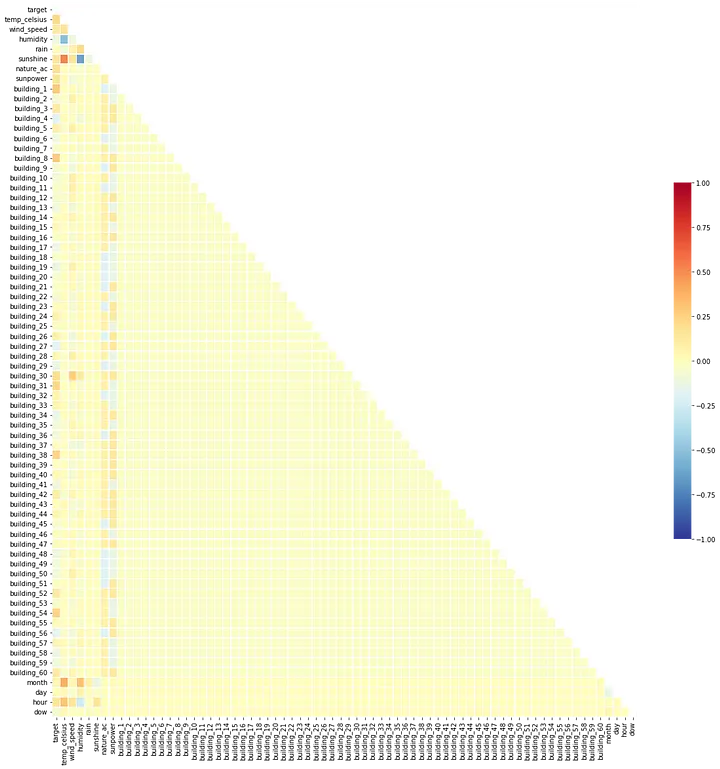
humidity(습도) ~temp_celsius(섭씨온도)- 상관계수:
-0.5091 - 약한 음의 상관관계를 가진다고 보는 것이 맞아보인다.
- 상관계수:
 ~ temp_celsius(섭씨온도).webp)
humidity(습도) ~ temp_celsius(섭씨온도)
sunshine(일조) ~temp_celsius(섭씨온도)- 상관계수:
+0.5157 - 약한 양의 상관관계를 가진다고 보는 것이 맞아보인다.
- 하나는 categorical, 다른 하나는 numeric 이므로 둘 중 하나를 drop할 수 없다.
- 상관계수:
 ~ temp_celsius(섭씨온도).webp)
sunshine(일조) ~ temp_celsius(섭씨온도)
sunshine(일조) ~humidity(습도)- 상관계수:
-0.6276 - 약한 음의 상관관계를 가진다고 보는 것이 맞아보인다.
- 하나는 categorical, 다른 하나는 numeric 이므로 둘 중 하나를 drop할 수 없다.
- 상관계수:
 ~ humidity(습도).webp)
sunshine(일조) ~ humidity(습도)
(2) Pairplot
building_{##} 변수들을 제외한 채 visualize pairplot
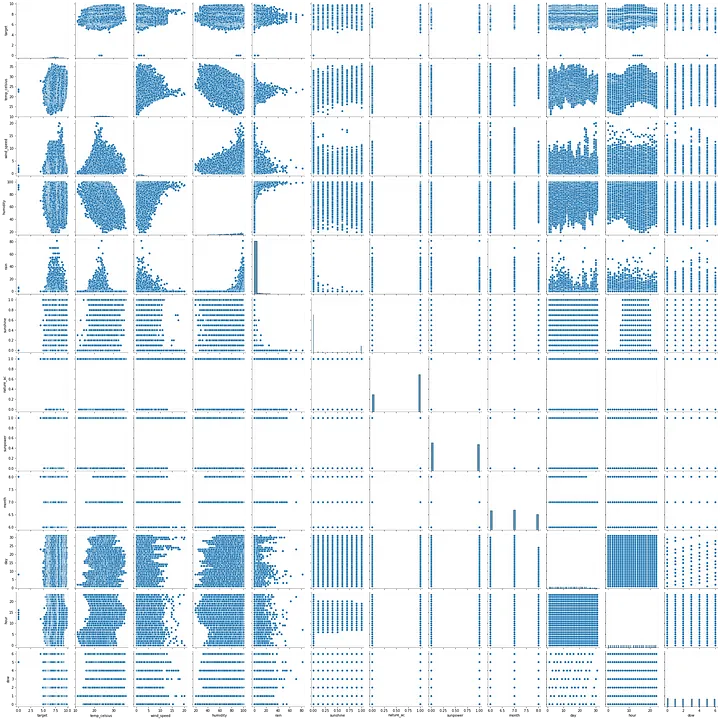
특정 하나의 독립변수가 Target에 절대적인 상관관계를 가지는 것이 관측되지 않는다.
(3) 각 독립변수들의 Distribution of Values
temp_celsius (섭씨온도)
- 비선형 변환 불필요
.webp)
AS-IS
wind_speed (풍속)
- log 변환 필요
-before-log.webp)
AS-IS
-after-log.webp)
TO-BE
humidity (습도)
- square root 변환 필요
-before-sqr.webp)
AS-IS
-after-sqr.webp)
TO-BE
rain (강수량)
- log 변환 필요
-before-log.webp)
AS-IS
-after-log.webp)
TO-BE
(4) 다중공선성(Multi-collinearity) 확인
VIF ≥ 10 에 해당하는 독립변수는 학습시 제외하도록 한다.
- “Variance Inflation Factors (분산팽창요인)”란?
특정 변수와 이미 높은 상관관계를 가짐으로써, 모델의 Overfitting에 영향을 끼칠 수 있는지를 측정하는 지표 일반적으로 VIF >= 5인 경우는 warning 신호, VIF >=10인 경우는 삭제 필요 신호
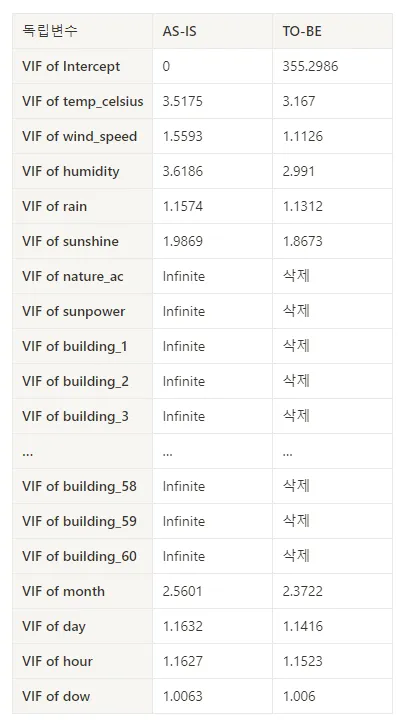
nature_ac,sunpower는 각building_##의 변수와 매우 높은 상관관계를 가지기 때문에 VIF = Infinite인 결과를 확인할 수 있었다.
(5) Outliers Handling
“평균값으로부터 3 Sigma 이상 편차가 발생하는 인스턴스를 모두 삭제하도록 한다.”
Box Plot of temp_celsius
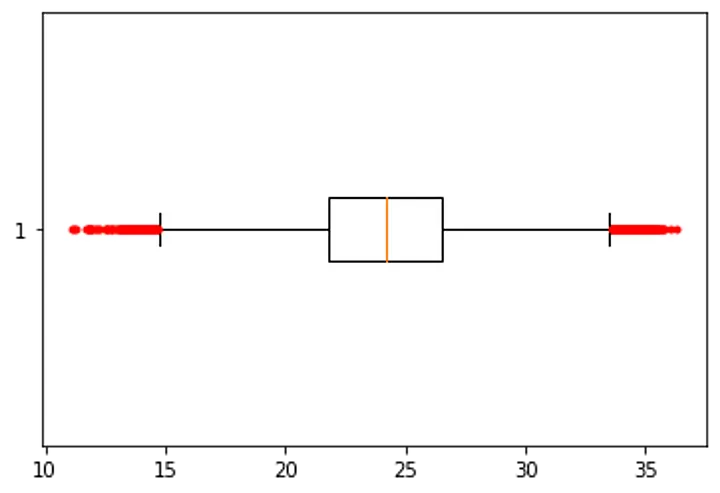
Box Plot of
temp_celsius
Box Plot of wind_speed
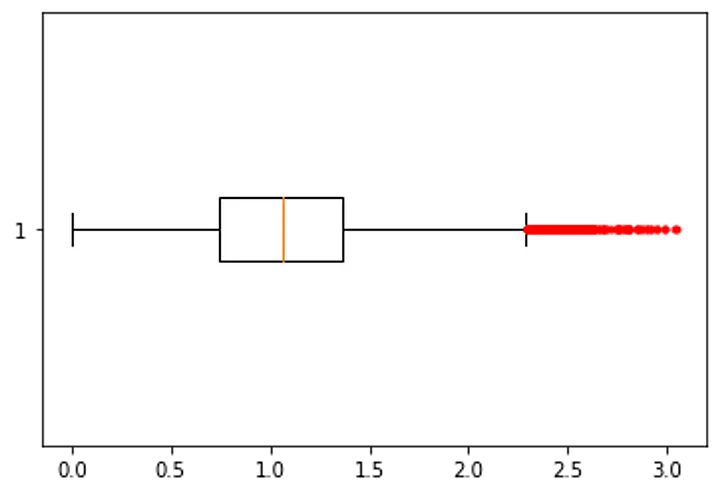
Box Plot of
wind_speed
Box Plot of humidity
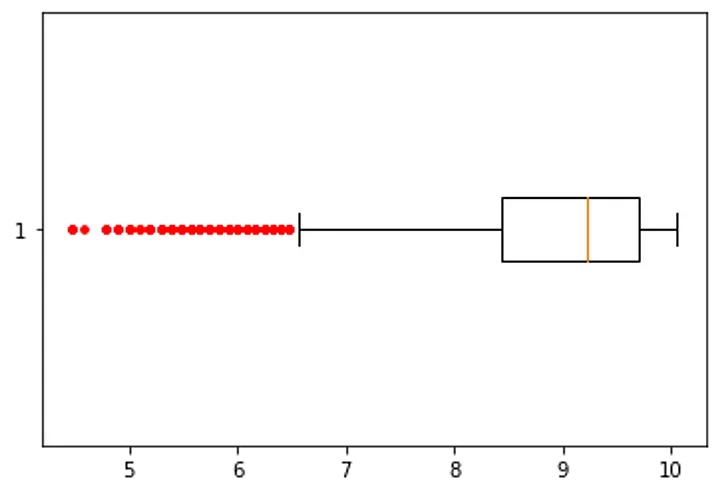
Box Plot of
humidity
Box Plot of rain
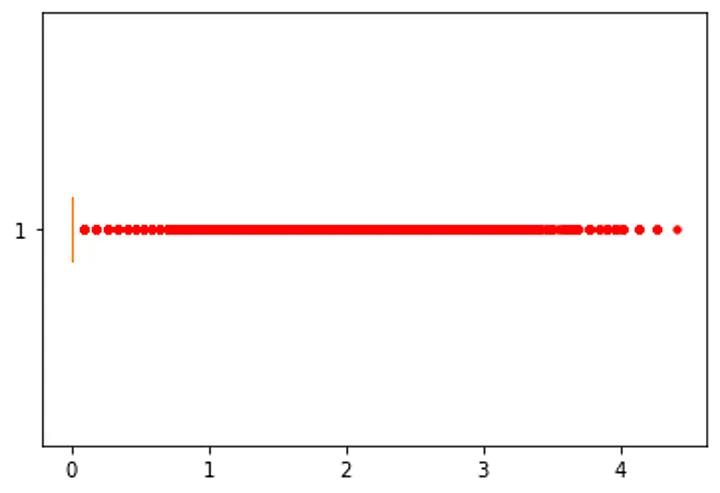
Box Plot of
rain
Box Plot of sunshine
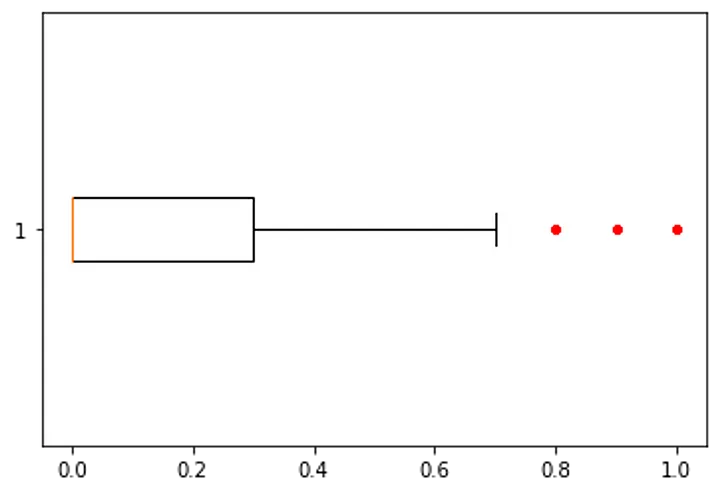
Box Plot of
sunshine
Box Plot of month, day, hour, and dow
- date_time 형식으로 이미 outliers 없이 골고루 분포되어 있으므로, Outliers Handling 불필요
“StandardScaler 모듈을 사용하여 모든 독립변수들을 정규화한다.”

mean = 0,std = 1의 표준정규분포로 변환
- “
-3 ≤ Scaled Value ≤ +3이 아닌 Feature가 1개라도 존재하는 인스턴스의 개수”- 5,589개 (약
4.57%) - 이 정도의 데이터 손실이라면, 오히려 제거를 하는 것이 Training에 유익한 결과를 낳을 것이다.
- 5,589개 (약
Pair Plot (After Removing All the Outliers)
.webp)
데이터의 국지적인 경향성이 상당 부분 제거가 되었다.
5. Modeling
5.1. Simple Linear Regression (v1)
lr = LinearRegression(n_jobs=-1)
lr.fit(data_input, data_target)
print('R-squared:', lr.score(data_input, data_target).round(4))
(1) Target 잔차 분석
-Target 잔차분석.webp)
[Residuals Plot] 잔차가 특정 패턴 없이 정규성을 잘 따르고 있는 것 같은데?
(2) 각 독립변수 잔차분석
오차항의 이분산성(heteroscedasticity) 없이, 잔차가 정규분포를 가장 잘 따르고 있다. 따라서 Polynomial or Logarithm을 즉각 적용해야 한다기보다, Regression Model 자체의 성능이 안 좋다는 것을 의미한다.
-각 독립변수 잔차분석.webp)
[Residuals Plot] 잔차가 특정 패턴 없이 정규성을 잘 따르고 있는 것 같은데?
-qq plot.webp)
[QQ Plot] 잔차의 분포가 정규분포에 가장 가깝네?
(3) Model Summary
model = smf.ols(
'target' + ' ~ ' + ' + '.join(data_input.columns),
data = data_df
).fit()
F-test의
p-value ≤ 0.05: 적어도 하나의 독립변수가 종속변수와 상관관계가 있다는 아주 강한 근거가 있다.
R-squared: 지나치게 낮아서 본 모델의 설명력이7.80%밖에 없다.
(4) Model의 Train Result & 유의성 지표
-result1.webp)
day변수 T-test의p-value ≥ 0.05: 제거하여 Refit Model 필요성이 있다.
(5) 독립변수별 Train Result & 유의성 지표
-result2.webp)
5.2. Simple Linear Regression (v2) — “day” 변수 제외
(1) Model Summary
model = smf.ols(
'target' + ' ~ ' + ' + '.join(data_input.columns.drop(['day'])),
data = data_df
).fit()
F-test의
p-value ≤ 0.05: 적어도 하나의 독립변수가 종속변수와 상관관계가 있다는 아주 강한 근거가 있다.
R-squared: 지나치게 낮아서 본 모델의 설명력이7.80%밖에 없다.
(2) Model의 Train Result & 유의성 지표
-result1.webp)
모든 변수가 T-test를 통과한다. (Confidence Level =
95%)
(3) 독립변수별 Train Result & 유의성 지표
-result2.webp)
day변수를 제외했음에도 불구하고, 모델의 설명력이 전혀 개선되지 않는다. 따라서, 본 Dataset에서는 Simple Linear Regression의 Training Capacity 자체가 매우 낮은 의미로 이해된다.
5.3. Polynomial Regression (v1) — “degree=2”
poly = PolynomialFeatures(degree=2)
poly.fit(data_input)
data_input_poly = poly.transform(data_input)
lr = LinearRegression(n_jobs=-1)
lr.fit(data_input_poly, data_target)
print('R-squared:', lr.score(data_input_poly, data_target).round(4))
# > R-squared: 0.1127
(1) 잔차분석
-잔차분석.webp)
Polynomial Regression (v1) — “degree=2”
5.4. Polynomial Regression (v2) — “degree=3”
poly = PolynomialFeatures(degree=3)
poly.fit(data_input)
data_input_poly = poly.transform(data_input)
lr = LinearRegression(n_jobs=-1)
lr.fit(data_input_poly, data_target)
print('R-squared:', lr.score(data_input_poly, data_target).round(4))
# > R-squared: 0.1362
(1) 잔차분석
-잔차분석.webp)
Polynomial Regression (v2) — “degree=3”
5.5. Polynomial Regression (v3) — “degree=4”
poly = PolynomialFeatures(degree=4)
poly.fit(data_input)
data_input_poly = poly.transform(data_input)
lr = LinearRegression(n_jobs=-1)
lr.fit(data_input_poly, data_target)
print('R-squared:', lr.score(data_input_poly, data_target).round(4))
# > R-squared: 0.1597
(1) 잔차분석
-잔차분석.webp)
Polynomial Regression (v3) — “degree=4”
5.6. Polynomial Regression (v4) — “degree=5”
poly = PolynomialFeatures(degree=5)
poly.fit(data_input)
data_input_poly = poly.transform(data_input)
lr = LinearRegression(n_jobs=-1)
lr.fit(data_input_poly, data_target)
print('R-squared:', lr.score(data_input_poly, data_target).round(4))
# > R-squared: 0.1806
(1) 잔차분석
-잔차분석.webp)
Polynomial Regression (v4) — “degree=5”
6. Conclusion
6.1. Regression Model 외의 모델이 필요하다!
(1) Modeling Results
| 회귀 모델 | 특이사항 | R-squared |
|---|---|---|
| Simple Linear Regression | 모든 독립변수 포함 | 0.0780 |
| Simple Linear Regression | day 독립변수 제외 |
0.0780 |
| Polynomial Regression | Up to 2nd Degree | 0.1127 |
| Polynomial Regression | Up to 3rd Degree | 0.1362 |
| Polynomial Regression | Up to 4th Degree | 0.1597 |
| Polynomial Regression | Up to 5th Degree | 0.1806 |
아무리 Capacity를 높여도 모델의 설명력이 극적으로 개선되지 않았다!
(2) Model Capacity
- Model Capacity란?
모델 용량: 다양한 차원의 관계성을 학습할 수 있는 능력 (The ability to fit a variety of functions) 🌝 간단히, 모델의 학습 가능 차수(차원)로 불리기도 함
- Models with Low Capacity: 학습 자체가 어려워진다. (
Underfitting문제) -
Models with High Capacity: Memory Effect의 부정적 효과가 발생한다. (
Overfitting문제) - Tree, Ensemble, Time-series 계열의 ML 모델들을 통해 접근하는 것이 적절해 보인다.
사실 이 Dataset은 Dacon에서 가져왔는데, Regression Model로 접근하는 사람들은 단 한 명도 없었다.
6.2. Regression Model이 해당 Dataset 학습에 적절한 모델이 아님을 파악하는 방법은?
(1) Simple Linear Regression의 잔차가 이분산성 없이 정규성을 매우 잘 따르는데도, R-squared 값이 매우 저조하다.
Simple Linear Regression: Target 잔차 분석
-Target 잔차분석.webp)
Simple Linear Regression: Target QQ Plot
-qq plot.webp)
(2) Polynomial Regression의 Degree를 높여도 잔차 자체가 개선되지 않는다.
Degree=2인 Polynomial Regression의 각 독립변수별 잔차
-잔차분석.webp)
Degree=5인 Polynomial Regression의 각 독립변수별 잔차
-잔차분석.webp)
Published by Joshua Kim
